Spatial enhancements to boost learning of science and math

Introduction

Science, Technology, Engineering, and Mathematics (called STEM subjects in the United States) are more than a body of knowledge. They are also a cast of mind: an approach to thinking, problem-solving, and developing and testing solutions. Advances in STEM drive economic prosperity and address pressing societal challenges – most recently the rapid development of the Covid-19 vaccine. Society needs innovative scientific, mathematical, and engineering minds that can use evidence-informed reasoning to solve challenging problems. STEM competencies are essential not only for solving societal problems (e.g., public health crises, developing clean-energy technology and solutions), but also for being an informed citizen, someone who can think critically and logically, navigate increasingly sophisticated technology, and synthesize large bodies of information (National Science and Technology Committee [NSTC], 2018). STEM education is crucial for preparing the workforce of tomorrow. Attempts to improve math and science teaching and learning often overlook a critical building block of STEM success: spatial thinking (Newcombe, 2010; 2013; Wai, Lubinski, & Benbow, 2009; Shea, Lubinski, & Benbow, 2001). Decades of research suggest that bridging the science of spatial thinking with educational practice holds great promise for improving science education (Gagnier & Fisher, 2020; Newcombe, 2017; Wai & Uttal, 2018). Yet teachers are not trained to teach spatially: to engage in classroom instruction that simultaneously builds students’ spatial thinking skills and STEM knowledge.

What is spatial thinking and why is it important?

Spatial thinking refers to a set of mental skills that enable us to reason about space and the relationships among and between objects. We rely on spatial thinking in daily life when we search for specific locations (e.g., where is the supermarket in relation to the library?), use representations of space (such as maps), or imagine what an object might look like rotated or resized. These skills are essential not only for daily life but also for success in STEM fields. Over 60 years of research has suggested spatial-thinking skills are uniquely important for success in STEM. Research has shown that:

• Spatial skills in middle and high school predict future STEM success.
• Spatial-thinking skills can be trained.
• Improving students’ spatial thinking can improve STEM outcomes.
• Spatial skills are an important component of school readiness and early math skills.

Spatial skills in middle and high school predict future STEM success

Spatial-thinking skills correlate strongly with students’ entrance into, retention in, and success within STEM disciplines (Shea et al., 2001; Wai et al., 2009). For example, the Project Talent study measured the spatial-thinking skills of 400,000 high-school students in a nationally representative sample in the 1960s and followed them for 11 years after high-school graduation. Students with high spatial-thinking skills were more likely to choose STEM majors in college, succeed within those majors, and choose to pursue STEM careers, compared to their peers with low spatial-thinking skills. This was true even after controlling for the fact that those students tend to have higher mathematical and verbal skills as well. Other longitudinal studies, in which students’ spatial-thinking skills were assessed in middle school and followed for 20 years (Shea et al., 2001), or in preschool and followed through high school (Wolfgang Stannard, & Jones, 2003), present similar findings.

Spatial thinking skills can be trained

Although spatial skills are often assumed to be innate, evidence from research suggests that they can be taught and improved (Uttal, Meadow, Tipton, Hand, Alden, Warren, & Newcombe, 2013). Intentional training can improve spatial-thinking skills in both children and adults, and the benefits of training are enduring and generalizable to new skills (Uttal et al., 2013). Studies point to three types of experiences that can facilitate spatial thinking: practicing spatial skills, such as mental rotation (imagining objects rotating in one’s head) for a period of time (e.g., from just 45 minutes to 1 hour per week over 12 weeks); playing video games, such as Tetris, for 1 hour per week for 12 weeks; or participating in semester-long courses that engage spatial reasoning, such as an engineering drafting course. Such training improves performance among a broad spectrum of students: those considered gifted and talented (Miller & Halpern, 2013); students with both high and low spatial-thinking skills (Terlecki, Newcombe, & Little, 2008), and males and females (Uttal et al., 2013). Spatial-skill development has been associated with engagement in spatial play activities, such as with puzzles, blocks, and shapes, among children under the age of seven (Jirout & Newcombe, 2015). This association holds even after controlling for other variables, such as parental education, that might influence this relationship.

Improving students’ spatial thinking can improve STEM outcomes

Emerging research suggests that bolstering students’ spatial thinking can improve academic achievement in chemistry (Small & Morton, 1983), engineering (Sorby, 2009), calculus (Sorby, Casey, Veurink, & Dulaney, 2013), elementary- and middle-school mathematics (Cheng & Mix, 2014; Lowrie, Logan, & Ramful, 2017), and physics (Miller & Halpern, 2013). In these studies, students complete a measure of STEM performance before and after training, and changes in performance are compared across groups who receive spatial training compared to another form of training. For example, six- to eight-year-old children improved their accuracy on mathematical calculation problems such as “3 + __ = 10” after having practiced mental rotation for 45 minutes. Children who had practiced crossword puzzles, in contrast, saw no such improvement (Cheng & Mix, 2014).

Spatial skills are an important component of school readiness and early math skills

There is a link between early mathematics skills and spatial reasoning, which suggests that the latter forms a component of school readiness (Verdine, Golinkoff, Hirsh‐Pasek, & Newcombe, 2017). For example, block-building skills are related to emerging math skills in preschool children. In one study, the research team gave three-year-olds a block model (several different colored Mega Bloks pieces, arranged in a specific configuration) and asked them to recreate the model using individual blocks. The team then compared accuracy on this task with general mathematical ability, such as asking children to count as high as they could without making a mistake or giving the researcher a specific number of objects, such as four crayons. The children who copied the block model more ably performed better on the math tasks. This finding is not causal, but it suggests that the relationship between spatial skills and math achievement begins as early as age three.

Why are spatial thinking skills important for STEM?

Why might spatial skills be important to students’ interest and achievement in the STEM fields? Scientific phenomena often involve spatial problems. Take, for example, Rosalind Franklin’s discovery of the structure of the DNA molecule: She inferred its three-dimensional structure from examining two-dimensional images. America’s K-12 students routinely confront spatial problems in science, mathematics, or engineering classes. Understanding the phases of the moon, visualizing chemical structures, learning about plate tectonics, and reading a graph all rely upon understanding spatial information and phenomena. For students to solve STEM problems, they must be able to understand and reason about the spatial properties of objects (e.g., location, size, volume). They also must be able to use visualizations (e.g., maps, graphs, and diagrams) to understand and reason about spatial relations that are often unable to be directly observed (e.g., molecules, tectonic plates, forces).

For instance, students may be asked to use diagrams, such as Figure 1, to understand forces and to predict how changes in forces can influence the motion of an object. To use this diagram, a student must (1) relate the lines in the diagram to three-dimensional objects; (2) understand that the size and direction of the arrows indicate the force being applied to the object; (3) reason about how these elements interact with one another; and (4) visualize and predict how changes to the forces will affect the object’s movement.

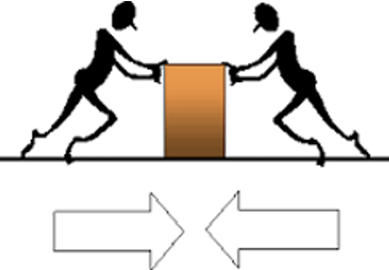
Figure 1. A diagram illustrating why a balanced force is an object at rest. The arrows’ size and direction indicate the strength and direction of the force being applied to the box.

Similarly, imagine a geometry student solving the problem shown in Figure 2. To solve this problem, the student must interpret the diagram to find the area of the frontmost triangle and then multiply that area by the depth of the entire figure.

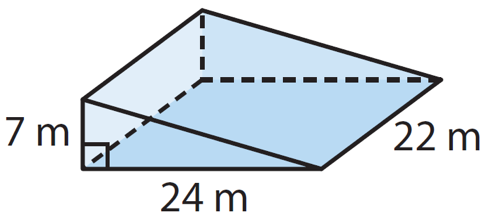
Figure 2. Find the volume of the prism shown above. Credit: www.onlinemath4all.com.

The importance of spatial thinking in STEM education raises a critical concern: What happens if students lack foundational spatial-thinking skills needed to do well in STEM? We know from a wealth of evidence that individuals vary dramatically in spatial skills, which have implications for student learning (Shea et al., 2001; Wai et al., 2009).

How do we foster spatial skills in the classroom?

Despite decades of research illustrating the importance of spatial thinking for success in STEM, few attempts have been made to incorporate spatial thinking in education (Newcombe, 2010; 2013; Taylor & Hutton, 2013), particularly in the elementary grades. When bringing spatial thinking to the classroom, it is important to recognize that classroom time is already too precious to set aside dedicated “spatial thinking activity time” for most schools. Instead, we can integrate these skills and activities into existing instructional time.

What can teachers do?

A potentially promising approach is to help teachers teach spatially. Teaching spatially involves engaging in instruction and classroom practices that build students’ spatial-thinking skills and STEM knowledge at the same time. Teaching spatially involves (1) identifying the spatial elements of a STEM concept or practice and how spatial thinking is used by the student to solve the problem; and (2) using five spatial enhancements to teach and learn STEM concepts and practices.

Identifying the spatial elements of a STEM concept or practice and how spatial thinking is used by the student to solve the problem

For example, imagine a population geography student asked to use Figure 3 to make a claim about how World War I and II affected life expectancy in Germany. To identify the spatial elements of the STEM concept or practice, the student needs to interpret the spatial patterns in the graph, notably that each axis has an orientation (down/up or left/right) and that these are essential for interpreting the graph. On the y-axis, up means higher: The higher the line, the greater the life expectancy. On the x-axis, time is chronologically moving from left to right. The farther to the left, the more recent in time.

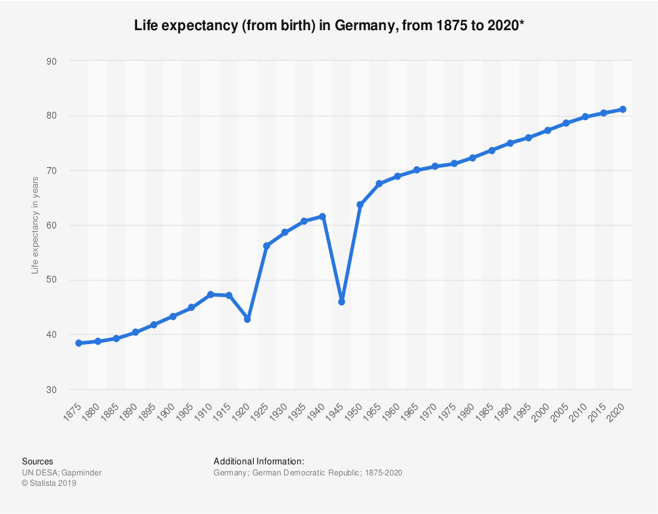
Figure 3. A graph depicting the average life expectancy in Germany from 1875 to 2020.

How is spatial thinking used by students to solve the problem? The height of the line in the graph and whether it increases or decreases tells the student about the pattern of life expectancy from 1875 to 2020. A decreasing line would indicate a decrease in life expectancy, and an increasing line would indicate an increase in life expectancy. Overall, the pattern of the line indicates that life expectancy has increased from 1875 to 2020, apart from two salient dips (or decreases) in 1920 and 1945. To answer the question, the student has to use these “dips” to make a conclusion about life expectancy during both world wars.

Using five spatial enhancements to teach and learn STEM concepts and practices

Research on spatial thinking and education has identified five spatial tools or learning enhancements that can build spatial skills and support students’ STEM content learning (see Gagnier & Fisher, 2020, for details). These are simple, free, engaging, and adaptable to many types of classrooms, both formal and informal:

Figure 4. A picture of a capuchin monkey (top) and beaver (bottom), oriented so the shape and structure of the tails can be compared.

• Explain visualizations to students: Visualizations, such as graphs and diagrams, are commonly used in STEM to illustrate information that is difficult to gain from words or direct experience (e.g., a graph showing sunset time across the year, or a diagram of the structure of the Earth). While common, visualizations are often challenging for students to interpret. Providing instruction on how to create and interpret their spatial patterns supports learning (Cromley, Bergey, Fitzhugh, Newcombe, Wills, Shipley, & Tanaka, 2013).
• Draw spatial properties, processes, or observations. Drawing to observe, document, reason, and problem-solve is a common practice by scientists and engineers, yet students often are not given the opportunity to draw in STEM learning (Ainsworth, Prain, & Tytler, 2011). Drawing can promote engagement and can help students observe, record, and think about the spatial properties of important concepts. Both students and teachers can draw. For example, imagine a student learning about how tail shape is an adaptation to survive in a specific environment. Students may be shown a picture of two different tails (beaver and capuchin monkey) and asked to draw them. The act of drawing can help students observe that the beaver’s tail is wide and flat (helpful for making dams), and the monkey’s tail is narrow and curvy (helpful for curling around trees).
• Use gestures to showcase spatial properties of concepts and practices. Gestures – intentional movements of the arm or head to express an idea or meaning – can support student learning in math and science (Crowder, 1996; Goldin-Meadow, 2011). Gestures can be used to communicate and reason about spatial elements of STEM concepts or problems. For example, imagine students orienting their hands to show y- and x-axes when learning about graphs? The teacher might ask, ‘Which way does the X-axis face?’ Students gesture a horizontal hand that is parallel to the floor. For the y-axis, they gesture a vertical hand that is perpendicular to the floor.
• Students and teachers can compare spatial features and properties of concepts. When students and teachers compare two objects, pictures, or entities, their differences and similarities become apparent (Gentner & Smith, 2012). For example, in Figure 4, notice the pictures of the capuchin monkey and beaver. By placing these images together, the differences in their tail shapes (wide vs. narrow, flat vs. curvy) and similarities (both near the bottom of the animal) become apparent.
• Use spatial language to describe observations, processes, and findings. Spatial language is the use of terms that describe the spatial properties and organization of the world (e.g., “on”, “greater than”, “diagonal”, “wide”, “flat”, “curvy”, “perpendicular”, “vertical”). These words can guide students’ attention (Pruden, Levine, & Huttenlocher, 2011) and support observation and learning.

Putting enhancements into action: an illustrative example

To provide an illustrative example of how a teacher might use these enhancements together to support learning, consider a lesson aimed at building third graders’ understanding of how weather tools are used to provide data on various types of weather (e.g., a rain gauge provides data on the amount of precipitation in a region). To use spatial enhancements while teaching these concepts, a teacher may demonstrate how the rain gauge works. A teacher would show a picture of a rain gauge and use gestures (see Figure 5) and spatial language to describe the shape of the rain gauge (narrow, tall, hallow, with an opening at the top), demonstrate how it collects rain, and show how the water level increases over time as it continues to rain.

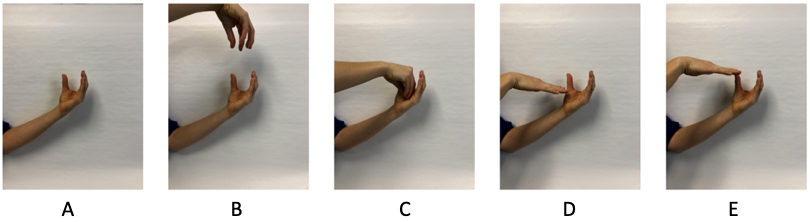
Figure 5. An illustration of a temporal sequence of gestures a teacher can use to explain how a rain gauge works.

To demonstrate how a rain gauge works with gestures and spatial language, the teacher first uses their hands to show an empty rain gauge (Panel A: Hand is cupped with an opening at the top to represent the rain gauge). The teacher then places a top hand (representing rain) over the bottom hand (representing the rain gauge) and lowers it into the bottom hand while fingers twinkle back and forth to represent rain falling from the sky down into the rain gauge (Panel B). Then the top hand moves all the way down into the bottom of the cupped hand to indicate rain falling to the bottom of the gauge (Panel C). The teacher then moves the top hand to represent the low level of the water in the gauge if it has just begun to rain (Panel D). As it rains more, the gauge fills up with water, and the water level in the gauge begins to rise/increase (Panel E). Finally, the teacher explains that you can measure the height of water in the gauge, and that tells you how much it rained over time.

What can school and district level administrators do?

While the above examples have focused on teacher practices during classroom instruction, administrators and leaders play an essential role in teachers’ capacity to implement spatial enhancements in their classrooms. School leaders can:

• support teachers’ attempts to incorporate spatial enhancements in their classroom practices;
• provide professional development for teachers on how to implement spatial-thinking activities to build STEM knowledge and skills;
• partner with researchers and curriculum-developers to develop and test spatially enhanced curricula and approaches to teaching.

Incorporating spatial enhancements in teachers’ classroom practice

Teachers need to feel supported by school leaders and the broader school culture to try out various spatial-thinking approaches in their classroom. Leaders can help facilitate a school climate (Cohen, McCabe, Michelli, & Pickeral, 2009) that supports professional experimentation and betterment over teaching practices over time. Growing work has shown that supportive school leaders who champion programs, interventions, and novel approaches and who devote time to and encourage their implementation are essential to change at the classroom and school level (see Beets, Flay, Vuchinich, Acock, Li, & Allred, 2008). If leaders express support for teachers to teach spatially, this can improve teachers’ interest in and attitudes regarding incorporating novel approaches into their practice.

Professional development for teachers

There is a lack of training around the importance of spatial-thinking skills in teacher education and training programs, and, thus, to address this gap, administrators may provide hands-on, action-oriented professional development for teachers on how to implement spatial-thinking activities in their classroom. Professional opportunities for teachers around learning to teach spatially should include core features of effective teacher professional development: active participation, collaboration with colleagues, and periods of reflection on their own practices; content focus on a specific subject matter (e.g., how spatial thinking supports the mastery of science content knowledge and practices) and alignment with state standards and local district priorities and goals; sufficient duration over an extended period of time; and ample opportunities to receive feedback on their knowledge and skills from expert coaches or facilitators (Darling-Hammond, Hyler, & Gardner, 2017; Desimone, 2009; Desimone & Pak, 2017; Garet, Porter, Desimone, Birman, & Yoon, 2001).

Developing spatially enhanced curricula and approaches to teaching

Despite decades of research illustrating that spatial thinking is essential for success in math and science, few attempts have been made to translate research on spatial thinking into curricula and to evaluate the effectiveness of this approach on supporting student learning in math and science. Gagnier and Fisher (2020) describe a collaboration between researchers, school leaders, and curriculum-developers to translate spatial enhancements into a third-grade science curriculum. This curriculum is currently being evaluated for impact on bolstering student interest and achievement in science. More partnerships like these will advance the field and yield evidence-informed spatially enhanced teaching and learning practices.

Conclusion

In this essay, we have argued for the potential of working with teachers to use spatial enhancements in communicating about STEM material. The value of this approach still needs to be explored, beginning with evaluations in the real world of schools of whether interventions that target students’ spatial-thinking skills lead to improved outcomes in the classroom, and, if so, which interventions in what subjects at what ages. For instance, perhaps it is crucial to start early by equipping childcare and pre-K programs with spatially rich education centers that include blocks, puzzles, and two- and three-dimensional shape games, to nurture a capacity and an interest in science and math. Research is accumulating, but, as always, questions remain. There is less research on teacher preparation and in-service programs. What works to communicate practical skills in a context of understanding the overall rationale for spatial practices? Can professional development influence teachers’ attitudes and self-efficacy? There are beginning to be programs and experiments to address these questions, and we hope to know much more soon.

References

Ainsworth, S., Prain, V., & Tytler, R. (2011). Drawing to learn in science. Science, 333(6046), 1096–1097.

Beets, M. W., Flay, B. R., Vuchinich, S., Acock, A. C., Li, K. K., & Allred, C. (2008). School climate and teachers’ beliefs and attitudes associated with implementation of the positive action program: A diffusion of innovations model. Prevention Science, 9(4), 264–275.

Cheng, Y. L., & Mix, K. S. (2014). Spatial training improves children’s mathematics ability. Journal of Cognition and Development, 15(1), 2–11.

Cohen, J., McCabe, L., Michelli, N. M., & Pickeral, T. (2009). School climate: Research, policy, practice, and teacher education. Teachers College Record, 111(1), 180–213.

Cromley, J. G., Bergey, B. W., Fitzhugh, S., Newcombe, N., Wills, T. W., Shipley, T. F., & Tanaka, J. C. (2013). Effects of three diagram instruction methods on transfer of diagram comprehension skills: The critical role of inference while learning. Learning and Instruction, 26, 45–58.

Crowder, E. M. (1996). Gestures at work in sensemaking science talk. Journal of the Learning Sciences, 5(3), 173–208.

Darling-Hammond, L., Hyler, M. E., & Gardner, M. (2017). Effective teacher professional development. Palo Alto, CA: Learning Policy Institute.

Desimone, L. M. (2009). Improving impact studies of teachers’ professional development: Toward better conceptualizations and measures. Educational Researcher, 38(3), 181–199.

Desimone, L. M., & Pak, K. (2017). Instructional coaching as high-quality professional development. Theory into Practice, 56(1), 3–12.

Gagnier, K. M., & Fisher, K. R. (2020). Unpacking the black box of translation: A framework for infusing spatial thinking into curricula. Cognitive Research: Principles and Implications, 5(1), 1–19.

Garet, M. S., Porter, A. C., Desimone, L., Birman, B. F., & Yoon, K. S. (2001). What makes professional development effective? Results from a national sample of teachers. American Educational Research Journal, 38(4), 915–945.

Gentner, D., & Smith, L. (2012). Analogical reasoning. Encyclopedia of Human Behavior, 2, 130–136.

Goldin‐Meadow, S. (2011). Learning through gesture. Wiley Interdisciplinary Reviews: Cognitive Science, 2(6), 595–607.

Jirout, J. J., & Newcombe, N. S. (2015). Building blocks for developing spatial skills evidence from a large, representative US sample. Psychological Science, 26(3), 302–310.

Lowrie, T., Logan, T., & Ramful, A. (2017). Visuospatial training improves elementary students’ mathematics performance. British Journal of Educational Psychology, 87(2), 170–186.

Miller, D. I., & Halpern, D. F. (2013). Can spatial training improve long-term outcomes for gifted STEM undergraduates? Learning and Individual Differences, 26, 141–152.

National Science and Technology Committee (NSTC). (2018). Charting a course for success: America’s strategy for STEM education. Washington, DC: US Government.

Newcombe, N. S. (2010). Picture this: Increasing math and science learning by improving spatial thinking. American Educator, 34(2), 29.

Newcombe, N. S. (2013). Seeing relationships: Using spatial thinking to teach science, mathematics, and social studies. American Educator, 37(1), 26–31 and 40.

Newcombe, N. S. (2017). Harnessing spatial thinking to support STEM learning. Paris: OECD Publishing.

Pruden, S. M., Levine, S. C., & Huttenlocher, J. (2011). Children’s spatial thinking: Does talk about the spatial world matter? Developmental Science, 14(6), 1417–1430.

Shea, D. L., Lubinski, D., & Benbow, C. P. (2001). Importance of assessing spatial ability in intellectually talented young adolescents: A 20-year longitudinal study. Journal of Educational Psychology, 93(3), 604.

Small, M. Y., & Morton, M. E. (1983). Research in college science teaching: Spatial visualization training improves performance in organic chemistry. Journal of College Science Teaching, 13(1), 41–43.

Sorby, S. A. (2009). Educational research in developing 3‐D spatial skills for engineering students. International Journal of Science Education, 31(3), 459–480.

Sorby, S., Casey, B., Veurink, N., & Dulaney, A. (2013). The role of spatial training in improving spatial and calculus performance in engineering students. Learning and Individual Differences, 26, 20–29.

Taylor, H. A., & Hutton, A. (2013). Think3d! Training spatial thinking fundamental to STEM education. Cognition and Instruction, 31(4), 434–455.

Terlecki, M. S., Newcombe, N. S., & Little, M. (2008). Durable and generalized effects of spatial experience on mental rotation: Gender differences in growth patterns. Applied Cognitive Psychology, 22(7), 996–1013.

Uttal, D. H., Meadow, N. G., Tipton, E., Hand, L. L., Alden, A. R., Warren, C., & Newcombe, N. S. (2013). The malleability of spatial skills: a meta-analysis of training studies. Psychological Bulletin, 139(2), 352.

Verdine, B. N., Golinkoff, R. M., Hirsh‐Pasek, K., & Newcombe, N. S. (2017). I. Spatial skills, their development, and their links to mathematics. Monographs of the Society for Research in Child Development, 82(1), 7–30.

Wai, J., & Uttal, D. H. (2018). Why spatial reasoning matters for education policy. Washington, DC: American Enterprise Institute.

Wai, J., Lubinski, D., & Benbow, C. P. (2009). Spatial ability for STEM domains: Aligning over 50 years of cumulative psychological knowledge solidifies its importance. Journal of Educational Psychology, 101(4), 817.

Wolfgang, C., Stannard, L., & Jones, I. (2003). Advanced constructional play with LEGOs among preschoolers as a predictor of later school achievement in mathematics. Early Child Development and Care, 173(5), 467–475.