The numerical intuitions at early childhood support math achievement at school

Executive summary

• Humans are born with efficient systems to process the numeric aspects of the elements of the surrounding world.
• These abilities are conceived as part of a core system, which would serve as foundational for formal math achievement trained at the school.
• Preschoolers benefit from training approximate number computations, words numbers, large number comparison guessing, and other numeric playful games.
• The training of number intuitions and approximate number operations would contribute to reduce the socio-economic status-related gap in math achievement we observe even from preschool age.
• The training of numeric intuitions from early childhood would provide benefits, even to children showing different levels of skill in non-numeric abilities such as working memory, attention, spatial cognition, verbal skills.

Introduction

In infants and young children, the number knowledge is usually measured with tasks aimed at comparing the absolute quantities of auditory or visual stimuli, usually dots arrays in visual stimuli (Fig.1). The researchers look for behavioral responses, mainly longer looks toward the stimuli that respect or violate the child’s numeric expectations (which are also called “surprise”). Additionally, some studies measure the response of the brain during these tasks. Here, the intensity of the brain responses would indicate the child’s acuity detecting changes in the number of elements of the presented stimuli.

Fig. 1. A classic visual experimental protocol to evaluate the numeric skills in infants and young children consists in exposing the children to a series of images with dot arrays containing a certain number of elements, for instance, 8. After a habituation period with a certain quantity, the children are tested about their approximate numeric knowledge by exposing them to either an image containing the same number of dots i.e. 8, or a different number of dots, such as 16 in the current figure. If the child detects the change in the dots’ number in the testing image, they react with surprise and longer looking time toward the unexpected stimuli.

The precision to distinguish numerosity between visual stimuli rapidly develops during the first year, becoming more precise while the child grows up.

The numeric abilities of young infants and some of their brain correlates

Evidence of math knowledge has been observed from the neonatal period. Three-day-olds can match the number of sounds of an auditory sequence with the number of the objects the perceive in images¹. For instance, after hearing sequences of 4 sounds they look longer to images containing 4 objects over images containing 12 objects, and vice versa. This amazing skill remains when one of the numbers is at least 3 times larger than the other, such as 6 vs 18, but it disappears when the numbers are too close. Indeed, neonates fail to match the number of sounds and objects in an image when the images contain numbers such as 4 and 8. Together, these results show that humans have numeric knowledge just after birth, although those abilities are quite imprecise at this initial state. This limitation may be associated with the immaturity in any cognitive ability that participate to solve the numeric task, such as working memory or audiovisual processing.

The ability distinguishing number rapidly develops during the first year, becoming more precise. At six months, infants can distinguish 16 from 8 sounds (one is a double of the other) but failed discriminating 12 from 8 sounds (one is two thirds of the other), while 9-month-olds can distinguish 12 from 8 sounds but not 10 from 8, indicating that infants advance to notice the difference between closer numerosities².

A few studies have evaluated the brain networks during numeric task in early infancy, using electroencephalogram, a non-invasive and safe technique to record the electrical activity generated by the brain. The electrical activity of the brain propagates throughout head tissues and can be safety recorded at the scalp.

One study evaluated the brain response associated with the detection of a change in the number of objects of a series of visual stimuli presented consecutively. The results showed that, when 3-month-olds detect a change in the number of the objects of the images, the brain activity increased over the electrodes placed over the right parietoprefrontal areas of the scalp (Fig. 2) ³. This results are very similar to the ones reported in adults.

Moreover, to some extent, the brain electrical activity recorded over the scalp can be used to estimate the brain areas contributing more to these responses by applying the so called source analysis. Interestingly, in the discussing study the source analysis unveiled brain networks very similar to one described in children older than 4 years and adults⁴, with the difference that in older children and adults the activation is greater over the left than in the right hemisphere⁵. These changes in the spatial distribution of the brain response illustrate a crucial property of the early neurocognitive development, that is, the intense reorganization of the brain circuits associated with the increase in age, experience and learning.

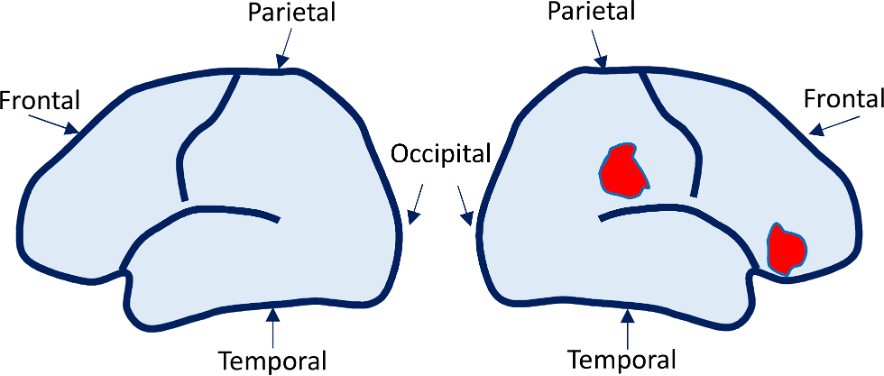
Fig. 2. This is a scheme of the electrical activity of the brain projected over the surface of the left and right hemispheres in a 6-month-old infant. The texts and arrows indicate the names of the lobes. The red dots illustrate the brain regions that would develop an increase in their electrical activity when detecting changes in numerosity. The regions correspond to the right parietal and prefrontal areas, which in children older than 4 years and adults involves the same areas but greater over the left hemisphere.

Other studies have also shown that the brain of 6- to 7-month-olds have networks particularly tuned to respond to stimuli with few (1 to 3) and many objects (8 to 32)⁶. These networks would be also quite similar to the ones described in adults doing similar tasks⁷.

Beyond discriminating numbers, infants also exhibited skills to correctly manage basic math operations such as sums, when the numbers are small i.e. less than 4. A pioneer study reported that 5-month-old infants can solve simple sums. Indeed, after seeing that two objects are placed behind an occluder, infants expect to see two objects when the occluder is removed and they are surprised when they see only one object⁸.

The infant brain also provides a neural correlate about this elementary arithmetic ability, which involves the management of abstract concepts. Using an object sum protocol, it is reported that when infants detect errors in the sum, such as when they perceive one object instead of two after the occluder is removed, the infant’s brain develops the so-called error response⁹, which is very similar to the one observed in adults when noticing own error¹⁰ or perceiving external erroneous information¹¹. Between others, the source of this error response would involve attention areas, such as the anterior cingulate cortex¹⁰. Moreover, error detection response would involve other networks participating in the detection of conflict between the current and the expected information¹².

Additionally, a rudimentary intuitive notion of order number is observed at 11 months of age, when infants distinguish between sequences of stimuli with an ascending or descending number of elements¹³.

Moreover, 8 to 12-month-olds infants exhibit quite abstract numeric abilities, such as when selecting the larger amount of cookies from two possible locations, regardless of the individual size of the cookies. For instance, when exposed to two boxes, one containing less and the other with more amount of cookies, infants scroll to the box with the larger amount of cookies, regardless of the number of them¹⁴. Thus, infants can understand that a big cookie is more attractive than two small ones.

The above-mentioned studies are some examples of the amazing capacities that infants and preschoolers have about number knowledge. Together the data indicate that humans are born with capacities to process the numeric information of the world in an approximate way. This ability is limited in precision and does not depend on education. Importantly, the intuitive number processing allows young children to approximately compare and arithmetically manipulate numbers and magnitudes, and it recruits similar brain networks in infants, preschoolers, and adults. These characteristics have allowed scientists to propose that the intuitive number knowledge is a component of a primitive core system of human cognition. The numeric properties of the surrounding world would be thus facilitated by prior knowledge about what numeric quantities and amounts are perceived and processed¹⁵.

Another relevant fact about the approximate number skills is that other non-human animal species also succeed in estimating numbers, indicating that number cognition may be a relevant skill for animal survival^15.

In humans, the intuitive number cognition abilities may serve as a pivotal capacity to advance in exact math thinking as the formal training made at the school. Formal math involves the training of math concepts such as division, and math symbols such as Arabic digits. Symbolic math allows solving exact computations, such as 4 divided by 3. Contrary to the approximate number computations, formal math is mostly learned at school and is quite hard to master across cultures, educational systems, and socioeconomic levels.

What is hard in number cognition during early development

Despite the abilities of infants to solve approximate number tasks, advancing in exact math learning at preschool and school-age is quite hard.

One possibility of this difficulty would be related to the immaturity of symbolic thinking. Previous studies indicate that symbolic thinking is quite immature before 3-4 years of age¹⁶. Another possibility is related to the still immature development of language. Indeed, preschoolers would have difficulties handling word numbers when referring to sets of elements. Interestingly, children from 3 to 7 years, who has been only informally exposed to numbers, number words and number concepts at home, have good estimations about large numbers. For instance, in average, the children succeed to recognize that 321 is more than 123, 101 is more than 99, and 402 is more than 42^{17, 18}. These early capacities are related to the exposure to the literate world with word numbers and written numbers before attending to the school.  A third possibility would be related to certain overtraining of counting at the informal level. For instance, in many cultures, adults train preschoolers to count individually, i.e. one, two, three, etc., four but do not to train young children to manage the number referring to a set of elements. When showing three cats we frequently teach by saying: “look, there is one (showing an object), two (showing another object) and three (showing another object)” instead of teaching with: “look, here there are three cats (showing the set of three objects) and there three dogs (showing the set of three objects), forcing children to handle the concept of “three” without counting. Indeed, as adults, we usually solve arithmetic tasks without counting, for instance, manipulating concepts such as dozens.

In sum, the traditional training of preschoolers to count is an important step for number learning, however, it may much gain from the training of other aspects of formal math such as words numbers and words numbers generalized to any set of elements, verbal and written representations of large numbers, guessing about large numbers manipulations. These approximate guessing practices may better familiarize the children with the alphabet applied to master in exact numeric tasks. 

The relationship between the initial numeric abilities and math achievement.

Last decades scientists have dedicated a considerable amount of research to explore whether the initial approximate numeric abilities of infants and young children relate to the achievement in formal math trained at the school. This interest is in part associated with the possibility to design new interventions aimed at detecting numeric thinking difficulties at early ages, and providing preventive and remedial interventions for math difficulties as early as possible.

Some studies have reported a positive relationship between intuitive and formal math. For instance, one study with 3 to 5-year-olds showed that the acuity estimating which of two sets of dots has more dots positively correlates with their symbolic math knowledge¹⁹. Importantly, at this age, this relationship between approximate and symbolic knowledge would be independent of the verbal skills of the children and would be stronger in preschoolers who are near to starting the school²⁰.

It is important to notice that others studies failed to demonstrate this direct link, indicating that other cognitive abilities would explain the strength of the link. Indeed, solving symbolic math tasks requires the indemnity of several cognitive functions such as working memory, attention²¹, attention autoregulation²², among others. Even socio-economic and cultural environment has been described as a critical factor for symbolic math achievement²³. This complex context has provided new challenges to the experimental designs aimed at disentangling the contribution of the performance in approximate number intuitions over symbolic math achievement.

The malleability of the intuitive numeric abilities

Many studies indicate that early numeracy intuitions are malleable, and as such, their training offers an important tool to promote numeric cognition from early ages. Several playful mathematics interventions have been used to provide children with informal opportunities to practice formal math notions. For example, preschoolers gain more in math achievement after a 3-weeks intervention, 15 min per day, when the intervention involves playing to compare larger numbers than when children receive classic math lessons on the same subject²⁴. Moreover, the children’s engagement with numeric games at home, such as playing with board games to compare numbers, highly predicts children’s math achievement at school²⁵. A crucial factor at home is the involvement of adults in the training game, by guiding, supervising, controlling the playing time, and providing explicit information about the importance of what the children gain by playing and practicing their numeric intuitions.

These types of intervention have been particularly beneficial for children from low socio-economic status, maybe because some data suggest that low-income families engage less in informal math training activities at home than middle-income families²⁶. Thus, playing math games at home and informal contexts would promote math readiness.

Furthermore, another type of study has explored the causal relationship between the training of the intuitive number abilities and math achievement. These studies have mainly used longitudinal pre-post experimental designs. In this type of experimental design, the participants are evaluated about their intuitive numeric abilities, math knowledge, and other cognitive abilities such as language or working memory, before and after an intervention, which trains only the intuitive numeric skills. Usually, the intervention develops across several days, although beneficial results have been described even during a single session. The key aspect in this type of study is that they must simultaneously evaluate several control groups, either trained in non-numeric abilities or not trained at all. Moreover, the children from the different groups must not differ in any other aspect, such as gender, age, socioeconomic status, other cognitive abilities such as working memory, attention or verbal skills, between others. Under these conditions, the comparison of how much the participants of the groups trained on intuitive math, other non-numeric abilities, or not trained gain in symbolic math allow the scientists to prove the benefits of the training of intuitive number cognition over formal math achievement.

Some studies have shown that the training of approximate number comparison and approximate sum associate with greater gain in symbolic math. The benefits of this type of training have been reported for healthy young adults²⁷; preschool children²⁸, and first-grade children²⁹.

Importantly, the training in approximate arithmetic sum associates with the activation of specific brain networks in young children. Indeed, evaluated with the electroencephalogram technique, which evaluates the electrical response of the brain when it propagates at the level of the scalp, first-grade children develop a higher brain response previously reported in adults when they are engaged in solving approximate sums. Moreover, this data show that the greater the accuracy to solve the approximate sums, the higher the intensity of this brain response³⁰ (Fig.3).

Fig. 3. The figure illustrates the trial of an experimental protocol aimed at measuring the brain response during an approximate arithmetic task. The brain response is recorded by using the electroencephalogram technique, which captures the electrical activity of the brain when solving the task. In A) we illustrate the steps of the trials. The children are exposed to two events showing that two groups of dots move behind an occluder, and then see a final image containing the sum of the all dots that previously moved behind the occluder or a different number of dots. Different groups of children must solve different tasks about the same stimuli. One group of children must decide if the dots in the target image (the last one) had more or fewer dots than the sum of all the dots placed behind the occluder. This task involves solving an approximate number sum. Another group of children must decide if the color of the dots in the target image was more similar to the color of the first or the second group of dots, by applying an approximate color comparison reasoning. In B) we show a brain response classically explored for approximate arithmetic, recorded over the parietal electrodes. In C) we can see that the brain response (averaged across all children) for each group is quite different over the parietal electrodes, indicating that the brain networks recruited to solve each task also differ.

More recently, a large study involving 1540 children mostly aged between 4 and 5.5 years, from low socio-economic level, showed that a 4-months intervention aimed at training the approximate number computations benefits symbolic math but only at short-term³¹. Indeed, evaluated a year after the intervention finished, children show no significantly greater gain in their formal math capacities. This type of result indicates that even if provides beneficial effects at short-term, the training of the approximate number intuitions is not enough to trigger radical changes in the child’s math thinking that facilitate formal math learning at school. These results are not discouraging for research in the field, in contrast, they only have opened the mind of educators and scientists, who have started exploring other protocols that may be more successful.

Recent researches are evaluating whether the concurrent training of the approximate and exact numeric computations may be more efficient to generate long-term benefits over math achievement at the school. For instance, in the image at the right, if you ask the child “add the blue, pink and green dots” she will probably start counting. However, by adding circle surrounding groups of ten dots, the child may become familiar with the notion of dozens and start to use base-ten structures to solve the sum.

Because the training of approximate arithmetic has also shown benefits for symbolic math in young adults²⁷, it is possible that this type of intervention may have a greater impact if it is regularly applied across the school years. Additionally, no intervention of this type has shown negative effects on child development, which makes it an interesting tool to promote number cognition from early ages.

Message to early childhood educators

In sum, humans are born with the ability to mentally process numbers in an approximate way. This ability rapidly develops during the first years even before the children go to school. Several studies have shown that a greater performance to estimate numbers during infancy and preschool age predicts higher math achievement. Other studies have demonstrated that the training of approximate arithmetic also benefit math knowledge in 4.5-year-old preschoolers. These beneficial effects are higher in children who are near attending school³². An important fact is that none of the studies evaluating the training of approximate number comparison and approximate arithmetic sum have reported negative effects for children. Thus, although the optimal conditions to better exploit the numeric intuitions to promote math achievement remain under research, the practice of playing and training the approximate number abilities seems to provide only benefits to children and may serve as an efficient educational tool for early childhood educators.

Message to policymakers

Promoting an integral cognitive development at preschool age is crucial for the development of nations at long-term. It is demonstrated that the investments during this period generate higher benefits probably because children’s brains develop most rapidly at these ages or because young children have more efficient learning strategies, such as the ones underpinning one-shot learning. Policy makers must consider that any gain in cognitive skills and learning mechanisms obtained before attending school, will potentiate the success of formal learning at school, and that any gain in school achievement will potentiate the development of citizens who will have better jobs, higher salaries, better health, greater sense of wellbeing

References

1. 1. 10382–10385. doi.org/10.1073/pnas.0812142106 (2009).
   2. Lipton JS, Spelke ES. Origins of number sense. Large-number discrimination in human infants. Psychological Science, 14, 396-401. doi: 10.1111/1467-9280.01453. (2003)
   3. Izard, V., Dehaene-Lambertz, G., Dehaene, S. Distinct cerebral pathways for object identity and number in human infants. PLoS Biology, 6, e11. (2008).
   4. Cantlon, J., Brannon, E., Carter, E., Pelphrey, K. Functional imaging of numerical processing in adults and 4-y-old children. PLoS Biology 4, e125 doi:10.1371/journal.pbio.0040125 (2006).
   5. Hyde, D. C., Boas, D. A., Blair, C., Carey, S. Near-infrared spectroscopy shows right parietal specialization for number in pre-verbal infants. NeuroImage 53, 647–652 (2010).
   6. Hyde, D. C., Spelke, E. S. Neural signatures of number processing in human infants: evidence for two core systems underlying numerical cognition. Developmental Science, 14, 360-371. doi: 10.1111/j.1467-7687.2010.00987.x. (2011).
   7. Hyde, D.C., Spelke, E.S. All numbers are not equal: an electrophysiological investigation of large and small number representations. Journal of Cognitive Neuroscience, 21, 1039–1053. (2009).
   8. Wynn, K. Addition and subtraction by human infants. Nature 358, 749–750. doi.org/10.1038/358749a0 (1992).
   9. Berger, A., Tzur, G., Posner, M I. Infant brains detect arithmetic errors. Proceedings of the National Academy of Sciences, 103, 12649-12653; DOI: 10.1073/pnas.0605350103. (2003).
   10. Carter CS, Braver TS, Barch DM, Botvinick MM, Noll D, Cohen JD. Anterior cingulate cortex, error detection, and the online monitoring of performance. Science, 280, 747-749. doi: 10.1126/science.280.5364.747 (1998).
   11. Hald, L. A., Bastiaansen, M. C. M., Hagoort, P. (2006) Brain and language. 96:90–105. (2006).
   12. Yeung, N., Botvinick, M. M., Cohen, J. D. The neural basis of error detection: conflict monitoring and the error-related negativity. Psychological Review. 111, 931-959. doi: 10.1037/0033-295x.111.4.939. PMID: 15482068. (2004).
   13. Brannon, E. M. The development of ordinal numerical knowledge in infancy. Cognition, 83, 223-40. (2002).
   14. Feigenson, L., & Carey, S. On the limits of infants’ quantification of small object arrays. Cognition, 97, 295–313. doi.org/10.1016/j.cognition.2004.09.010 (2005).
   15. Feigenson, L., Dehaene, S., Spelke, E. (Core systems of number. Trends in Cognitive Sciences, 8, 307–314. doi.org/10.1016/j.tics.2004.05.002 (2004).
   16. Deloache J. S. Becoming symbol-minded. Trends in cognitive sciences, 8, 66–70. doi.org/10.1016/j.tics.2003.12.004
   17. Mix, K. S., Prather, R. W., Smith, L. B., Stockton, J. D.. Young children’s interpretation of multidigit number names: from emerging competence to mastery. Child Development, 85, 1306-1319. doi: 10.1111/cdev.12197. (2014)
   18. Libertus, M. E, Odic, D., Feigenson, L., Halberda, J. The precision of mapping between number words and the approximate number system predicts children’s formal math abilities. Journal of Experimental Child Psychology, 150,207-226. doi: 10.1016/j.jecp.2016.06.003. (2016).
   19. Libertus, M. E., Feigenson, L., Halberda, J. Preschool acuity of the approximate number system correlates with school math ability. Developmental Science, 14, 1292-300. doi: 10.1111/j.1467-7687.2011.01080.x (2011).
   20. Wang, J. J., Halberda, J., Feigenson, L. Emergence of the Link Between the Approximate Number System and Symbolic Math Ability. Child Development, 92, e186-e200. doi: 10.1111/cdev.13454. (2021).
   21. Chew, C. S., Forte, J. D., Reeve, R. A. Cognitive factors affecting children’s nonsymbolic and symbolic magnitude judgment abilities: A latent profile analysis. Journal of Experimental Child Psychology, 152, 173-191. doi: 10.1016/j.jecp.2016.07.001. (2016).
   22. Pomè, A., Thompson, D., Burr, D. C., Halberda J. Location- and object-based attention enhance number estimation. Atten Percept Psychophys. 83, 7-17. doi: 10.3758/s13414-020-02178-w. (2021).
   23. Starr, A., Brannon, E. Evolutionary and Developmental Continuities in Numerical Cognition. Evolutionary Origins and Early Development of Number Processing, 1, 123. 10.1016/B978-0-12-420133-0.00005-3. (2014).
   24. Ramani & Eason, 2015). Ramani, G., Eason, S. It all adds up. Phi Delta Kappan. 96, 27-32. 10.1177/0031721715583959. (2015).
   25. Lefevre, J. A. et al. Home Numeracy Experiences and Children’s Math Performance in the Early School Years. Canadian Journal of Behavioural Science/Revue canadienne des sciences du comportement, 41, 55-66. 1037/a0014532. (2009).
   26. Scalise, N. R., Daubert, E. N., & Ramani, G. B. (2017). Narrowing the Early Mathematics Gap: A Play-Based Intervention to Promote Low-Income Preschoolers’ Number Skills. Journal of numerical cognition, 3, 559–581. https://doi.org/10.5964/jnc.v3i3.72).
   27. Park, J., Brannon, E. M. Training the approximate number system improves math proficiency. Psychological Science. 24, 2013-9. doi: 10.1177/0956797613482944. (2013).
   28. Libertus ME, Odic D, Feigenson L, Halberda J. Effects of Visual Training of Approximate Number Sense on Auditory Number Sense and School Math Ability. Frontiers in Psychology, 11:2085. doi: 10.3389/fpsyg.2020.02085. (2020).
   29. Hyde, D. C., Khanum, S., Spelke, E. S. Brief non-symbolic, approximate number practice enhances subsequent exact symbolic arithmetic in children. Cognition, 131, 92-107. doi: 10.1016/j.cognition.2013.12.007 (2014).
   30. Gouet, C., Gutiérrez-Silva, C., Guedes, B., Peña, M. Cognitive and Neural Effects of a Brief Nonsymbolic Approximate Arithmetic Training in Healthy First Grade Children. Frontiers in Integrative Neuroscience, 12, 28. 10.3389/fnint.2018.00028 (2018).
   31. Dillon, M. R., Kannan, H., Dean, J. T., Spelke, E.S., Duflo, E. Cognitive science in the field: A preschool intervention durably enhances intuitive but not formal mathematics. Science, 357, 47-55. doi: 10.1126/science.aal4724. (2017).
   32. Wang, J. J., Halberda, J., Feigenson, L.. Emergence of the Link Between the Approximate Number System and Symbolic Math Ability. Child Development, 92, e186-e200. doi: 10.1111/cdev.13454 (2021).