Early proportional reasoning and probabilistic thinking predict math achievement at school

Executive summary

• Humans are born with intuitive abilities in proportional reasoning. Initially, the intuitive proportional thinking is difficult to evaluate mainly because the children still do not handle the verbal representations of the proportions and maybe because children are over-trained to count any numeric task, interfering with thinking about proportional relationships.
• The early intuitions about proportions predict the achievement in symbolic proportional reasoning in preschoolers, school children, and adults.
• Intuitive proportional reasoning can improve by training, and more importantly, the training of intuitive proportional reasoning is associated with greater gains in symbolic proportional reasoning, providing a promising educational tool to support proportion-related education.

Introduction

Before the first birthday, children can not only perceive the information provided by stimuli but also manipulate and interpret this information taking into account their own perspectives. Children succeed in computing probabilities, using symbols, generalizing ratios from the first year of age, and other sophisticated mental computations which underpin complex cognitive abilities such as proportional reasoning.

Proportional reasoning

Most studies about number knowledge during early development have evaluated the manipulation of absolute quantities, such as integers. Indeed, these studies have shown that from birth infants can approximately estimate absolute quantities which become more precise with age¹. These abilities are intuitive, initially inexact but becoming more precise with age, involve similar neural networks to the ones described in adults when solving approximate number comparison and approximate arithmetic, improve with training, and to some extent, their accuracy predicts math achievement at school².

In contrast, despite its high relevance in daily life, the research exploring how children process relative magnitudes and develop their proportional reasoning is very scarce, although recent studies have unveiled the importance of training these capacities from a very early age.

There is some agreement about the idea that processing absolute and relative amounts and quantities rest on quite different mechanisms. The absolute number processing is directly coded from the stimuli, e.g. when we say “there are three dogs”, we indeed perceive three animals. In contrast, proportional reasoning requires abstractions. In the previous example, if we say one-third of the dogs is mine we must represent the whole (the three dogs) but also the parts (one of the three dogs).

Thus, proportional reasoning refers to the capacity to process relative quantities in a quite abstract way. When we solve tasks such as dividing a cake into similar size parts, using a map to explore a landscape, applying concepts such as “a-third” or “10 percent”, we apply proportional reasoning, unveiling the ubiquity of this type of thinking in solving everyday life tasks. Importantly, the proportional reasoning evaluated at educational institutions by measuring the success to solve fractions and ratios is considered a crucial ability for math achievement at school and high education³.

Similar to that observed during absolute number processing, humans have proportional reasoning capacities from infancy. These capacities use an approximate format in infants and young children that is, they are not exact. Moreover, the performance in proportional reasoning can correctly predict the achievement in fraction operations at the school age⁴, and can be improved by training. Together, these properties of proportional reasoning have allowed educators and scientists to explore the possibility to develop instruments and interventions to evaluate proportional reasoning from early ages, be more accurate in detecting proportional reasoning delay, and design preventive and remedial interventions at preschool and initial school age.

The approximate proportional reasoning before the school age

Symbolic proportional reasoning, that is, the one which involves the use of digits and math operators, and allows exact proportional computations to succeed processing fractions and ratios, is typically taught at school by the 3rd grade⁵. Fractions involve the abstract representation of generalizations that are crucial to advance into a better comprehension of other math issues such as algebra⁶ and other relational concepts. It is widely accepted that fractions are particularly hard for learners and that take years to master, across many different cultures³.

In contrast, the approximate proportional reasoning is intuitive and there is evidence that it is already functional during the first year of age. For instance, 6-month-old infants discriminate two arrays containing two elements with different proportions of each⁷ (Fig. 1). The proportional reasoning at this age is quite imprecise. Indeed, 6-month-olds can detect a change in the proportion of dots of a particular color in arrays containing dots of two different colors. However, the infants succeed to make this detection only if the change involves a switch between proportions such as 4:1 to 2:1. In contrast, the infants fail to detect changes between 2:1 and 1.5:1 proportions.

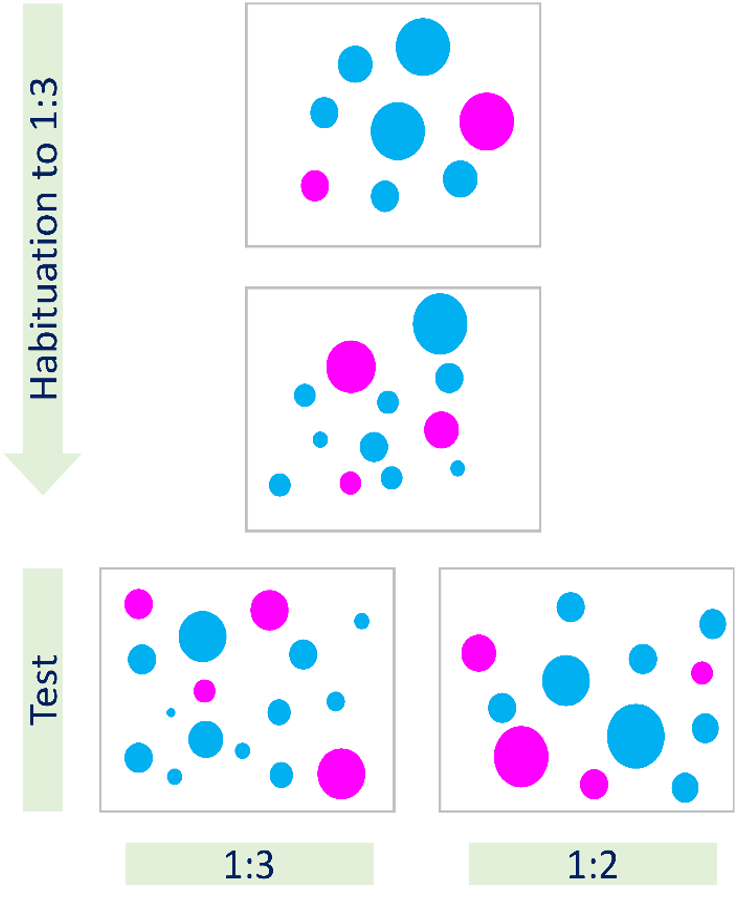
Fig. 1. The figure illustrates a classic experimental protocol to evaluate approximate proportions in 6-month-old infants. In a first step, the infants are habituated to a certain proportion by exposing them to different dot arrays containing dots of two different colors. In the image, we illustrate the habituation to the 1:3 proportion, where for each pink dot there are 3 cyano dots, regardless of the size and location of the dots. In a second step, infants are exposed to a test where they see either another array containing the same proportion of dots (1:3) or an array containing a different proportion such as the one in the image corresponding to 1:2 proportion, with 1 pink dot every 2 cyano dots. If the infants detect the change in the proportion they are surprise and look longer toward the array that violates their expectations created during the habituation phase.

At the same age, infants exposed to several images comprising a dowel and a jar with a constant size both, show surprise when the ratio between the dowel and its container sizes changed, but not when the absolute size of both objects changed while the ratio remain the same to the one they were habituated⁸. Similar results are found in 4-year-olds, who explicitly matched images with dowels and jars sizes having the same ratio⁹.

In preschoolers, 4-and 5-year-olds exposed to different stimulus composed of parts in different proportions, for instance, animals with a relatively small body or large head, correctly choose new animals that looks “just like” them, taking into account the proportional relationship of the parts¹⁰.

An important observation is that children aged at 6-years can succeed in estimating proportions but only when the amounts are presented in a continuous format, such as when the children must divide a pizza or a chocolate bar into equal parts¹¹. The processing of discrete quantities brings difficulties to proportional reasoning at an early age, probably because the children tend to count the parts of the stimuli and verbalize the procedure, somehow neglecting the relational analysis. Indeed, preschoolers mostly fail when they are called to divide amounts into halves, thirds or quarters¹². In contrast, they succeed when the task is presented in ludic contexts, using intuitive formats, and requiring minimal verbal demands.

For instance, four-year-olds, who do not yet master counting, can select correctly the recipient containing more marbles of a certain color from two available recipients containing two different proportions¹³, and 7-year-olds correctly predict how much happy would be a child when receiving a bag of jellybeans containing different proportions of her favorite flavor¹⁴. The success in these tasks is possible only when preschoolers are allowed to answer by pointing instead of speaking, indicating that a hard part of proportional reasoning involves their verbal representations.

Probabilistic thinking

To some extent, many of the abilities described above require intuitive probabilistic thinking. Indeed, probabilistic intuitions inherently require representing the computations of ratios¹⁵. Recent studies show that probabilistic thinking is functional in 12-month-old infants. When exposed to videos showing a Lotto-like recipient containing moving objects of different colors and shapes in different proportions, and having an opening site, which allows the exit of the objects, 12-month-olds make expectations about which object must exit by the opening. Indeed, infants are surprised when, after occluding the central part of the lotto, by the opening region appears the less numerous object (in the right image, the pink object), indicating that the infants computed not only the current proportions of the objects but also the probability of future events, based on which they make expectations.

Another evidence of the early capacities of infants involves 6.5-month-olds.  When exposed to images showing that a hand pushes a box toward the edge of a platform, they are surprised when only 15% of the box surface remains on the platform and they do not expect the box to fall when 70% of the surface stays in contact with the platform, neither when they see that a hand sustains the box even minimally touching the platform¹⁶.

In sum, there is strong evidence that humans have intuitive abilities to understand, process, and succeed in tasks involving the processing of proportional relationships between amounts and quantities, and that probabilistic intuition tightly relates to these skills. Similar to the approximate number computations, which humans can solve using absolute quantities (i.e. integers), the proportional abilities appear early in life and are quite imprecise in infancy, although develop with age. Contrary to that reported for absolute number knowledge, the study of proportional and probabilistic intuitions in infants and preschoolers has only recently acquired interest, partially because the intuitive proportional reasoning is considered a good predictor for posterior achievement in math at the school, and because recent studies have shown that it can be trained at early ages.

The link between intuitive and symbolic proportional reasoning

Until today only a few studies have evaluated the relationship between intuitive/approximate proportional reasoning and symbolic proportional thinking, evaluated through the ability to solve fractions, ratios, and formal relational numeric tasks.

One study found a positive relationship in young adults when comparing images containing two types of elements, in different proportions of each. The results showed that the students who showed higher performance in approximate comparisons also exhibited higher performance in symbolic fractions tests, evaluated using Arabic digits such as 5/7¹⁷. A second study showed similar results in involving fifth-graders, aged at 8 to 10 years4, although this link between approximate and symbolic proportional achievement tends to be weaker in children older than this age range¹⁸, probably because children start to apply other strategies to understand and solve these types of tasks with exactitude.

Thus, preschool-age would be a period of development particularly sensitive to promote intuitive proportional thinking, with the view that this training would provide foundational skills for further formal training at school.

Some authors have suggested that a part of the difficulties mastering symbolic proportional reasoning is the extreme efforts training counting and associating word numbers to written numbers. Children would thus develop a bias to process the numbers as absolute than as relational¹⁹. From this perspective, some initiatives have been proposed to train proportional reasoning from preschool and early primary school, and explore how much the children gain from that training.

Training proportional intuitions at early age benefits symbolic proportional reasoning

There are almost no longitudinal studies aimed at measuring the effects of training the approximate proportional reasoning on the symbolic proportional skills.

However, a recent study, developed by our group of research, explored this link in healthy 4th-grade children, aged between 9 and 10 years, applying a pre-post design²⁰.

The training comprised five 15-min long sessions of playing with a computerized training program. The stimuli for the training were designed taking into account the ones used in a previous study⁴ to measure the current ability to estimate proportional reasoning. The protocol showed children a series of images containing a recipient with different amounts of water and fruit. The child’s task was to decide for each image how tasty (i.e. fruity) would be the juice prepared by mixing the amounts of fruit and water shown in the image. The recipient was drawn in the image with the large dimension in the vertical axis. To answer, the child had to indicate the level of fruity of the juice in a horizontal line, scaled from no tasty at all to fully tasty, placed below the juice container (Fig, 3).

Fig. 3. Scheme of the stimuli designed to test the proportional reasoning using continuous amounts. The children see a series of images of a container representing different amounts of water and fruit (e.g. strawberry). To evaluate the approximate proportion reasoning the children are called to judge in each image how the juice prepared with the current combination of water and fruit tastes to the fruit (i.e. strawberry). They must provide their answer by moving a black vertical line across a grey bar representing a scale of taste, from very low to strongly tasty. In this type of study, it is important to evaluate children solving other control tasks using an identical set of stimuli to prove that the differences in performance relate to reasoning and not to the processing of any other eventual stimuli particularity. For instance, in this image, a control task asks the children to compare which is more, fruit or water. This task can be solved by comparing absolute amounts and should provide discrete answers.

Fig. 3. Scheme of the stimuli designed to test the proportional reasoning using continuous amounts. The children see a series of images of a container representing different amounts of water and fruit (e.g. strawberry). To evaluate the approximate proportion reasoning the children are called to judge in each image how the juice prepared with the current combination of water and fruit tastes to the fruit (i.e. strawberry). They must provide their answer by moving a black vertical line across a grey bar representing a scale of taste, from very low to strongly tasty. In this type of study, it is important to evaluate children solving other control tasks using an identical set of stimuli to prove that the differences in performance relate to reasoning and not to the processing of any other eventual stimuli particularity. For instance, in this image, a control task asks the children to compare which is more, fruit or water. This task can be solved by comparing absolute amounts and should provide discrete answers.

To measure how much the children gained by playing with this intervention, before and after the training the children completed a battery of assessments aimed at measuring their knowledge in symbolic proportional reasoning, symbolic math (arithmetic with absolute numbers), geometry, working memory, and verbal abilities. In parallel, another two groups of children, paired in age, gender, socioeconomic levels, and school achievement, were also evaluated. One of them was passive, comprised of children who did not play between pre and post-evaluations, although they did it after the intervention finished. A second group was active, comprised of children who were evaluated in a task that showed the same set of stimuli but asked t solve an approximate absolute comparison task. Indeed, each child must decide which amount was more, the fruit or the water, and provide a discrete answer using the same scale as the one used in the group solving proportional thinking.

The results of this brief intervention showed positive effects. The children who played with the proportional reasoning game gained more in several tasks: symbolic proportional reasoning, paper-and-pencil non-symbolic (approximate) proportional reasoning, and geometry. In contrast, not any control group showed significant gains in symbolic proportional reasoning or geometry. Together, the results indicate that the intuitive understanding of proportions is trainable in school children and that the training of approximate proportional reasoning benefits symbolic proportional reasoning and transfer to other math abilities such as geometry, at least when evaluated at short-term. Thus, the training of approximate proportional reasoning may be an efficient educative tool to promote math understanding and math achievement in the hard field of fraction and ratio learning.

Message to early childhood educators

Humans have intuitive abilities to understand, process, and succeed in tasks involving proportional reasoning from the first year of life.

The children unveil these early intuitions mostly when the tasks require minimal verbal demands, involve continuous amounts rather than discrete quantities, avoid counting, are presented in a ludic format, and allow no-verbal answers.

The early intuitions about proportions correlate with the achievement in symbolic proportional thinking in preschoolers, school children, and adults.

Brief ludic interventions can improve the intuitive proportional reasoning, and more importantly, can benefit the symbolic proportional reasoning, at least in short-term.

Together these data indicate that educating the intuitive proportional reasoning at the preschool age with ludic interventions can provide important benefits to the future understanding of fractions, ratio, and other relational concepts considered as pivotal for success in formal math education.

Importantly, promoting playful relational games at early ages must involve the schools, but also families and any social environment where the children grow and develop. Some societal initiatives have been already implemented in some cities with the idea of “learning landscapes”. The learning landscapes are placed in bus stops, parks, supermarkets, and other sites where children usually attend and play. Many learning games have 3D formats and seek to get the child’s attention to transmitting some basic concepts about reading, math, social, and reasoning. Initiatives like those illustrate that educators, scientists, and the general societies may implement interesting informal ways to provide opportunities to learn and promote education from early chilhood²¹.

Message to policymakers

The abilities that infants and young children develop before attending to school provide robust foundations for learning and lead to stronger academic achievement throughout the school period, and benefit wellbeing.

In several countries, economists have demonstrated the convenience of supporting high-quality nursery and preschool education for further development. For instance, in 2019 an economic report made in Australia demonstrate that for every dollar invested in early childhood education the country can receive two dollars back through higher tax revenues, higher wages, and productivity, and lower spending on welfare and criminal justice. Early childhood education is thus a unique opportunity to foster both, individual and national development.

References

1. Feigenson, L., Dehaene, S., Spelke, E. Core systems of number. Trends in Cognitive Sciences, 8, 307–314. doi.org/10.1016/j.tics.2004.05.002 (2004).
2. Starr, A., Brannon, E. Evolutionary and Developmental Continuities in Numerical Cognition. Evolutionary Origins and Early Development of Number Processing, 1, 123-144. 10.1016/B978-0-12-420133-0.00005-3. (2014).
3. Siegler, R. S., Fazio, L. K., Bailey, D. H., Zhou, X. Fractions: The new frontier for theories of numerical development. Trends in Cognitive Sciences, 17, 13-19. doi: 10.1016/j.tics.2012.11.004 (2013).
4. Möhring, W., Newcombe, N. S., Levine, S. C., Frick, A. Spatial proportional reasoning is associated with formal knowledge about fractions. Journal of Cognition and Development, 17, 67–84. doi.org/10.1080/15248372.2014.996289 (2016).
5. Siegler, R. S. et al. Early predictors of high school mathematics achievement. Psychological Science, 23, 691–697 (2012).
6. Lesh, R., Post, T., Behr, M. Proportional reasoning. In J. Hiebert, & M. Behr (Eds.). Number concepts and operations in the middle grades (pp. 93–118). Reston:
7. Lawrence Erlbaum & National Council of Teachers of Mathematics (1988).
8. McCrink, K., & Wynn, K. Ratio abstraction by 6-month- old infants. Psychological Science, 18, 740–745 (2007)
9. Duffy, S., Huttenlocher, J., Levine, S., Duffy, R. How infants encode spatial extent. Infancy, 8, 81–90 (2005).
10. Duffy, S., Huttenlocher, J., Levine, S. It Is All Relative: How Young Children Encode Extent. Journal of Cognition and Development, 6, 51–63. 10.1207/s15327647jcd0601_4) (2005).
11. Sophian, C. Perceptions of proportionality in young children: matching spatial ratios. Cognition, 75, 145–170. doi.org/10.1016/S0010-0277(00)00062-7 (2000).
12. Jeong, Y., Levine, S., Huttenlocher, J. The development of proportional reasoning: Effect of continuous versus discrete quantities. Journal of Cognition and Development, 8, 237-256 (2007).
13. Hunting, R. P., Sharpley, C. F. Fraction knowledge in preschool children. Journal for Research in Mathematics Education, 19, 175-180 (1988).
14. Yost, P. A., Siegel, A. E., & Andrews, J. M.. Nonverbal probability judgments by young children. Child Development, 33, 769–780 (1962).
15. Acredolo, C., O’Connor, J., Banks, L., Horobin, K. Children’s ability to make probability estimates: Skills revealed through application of Anderson’s functional measurement methodology. Child Development, 60, 933-945 (1989).
16. Téglás, E., Girotto, V., Gonzalez, M., Bonatti, L. L. Intuitions of probabilities shape expectations about the future at 12 months and beyond. Proceedings of the National Academy of Sciences of the United States of America, 104, 19156–19159. doi.org/10.1073/pnas.0700271104 (2007).
17. Baillargeon, R., Needham, A., Devos, J. The development of young infants’ intuitions about support. Early Development and Parenting, 1, 69–78. doi:10.1002/edp.2430010203 (1992).
18. Matthews PG, Lewis MR. Fractions We Cannot Ignore: The Nonsymbolic Ratio Congruity Effect. Cognitive Science, 41, 1656-1674. doi: 10.1111/cogs.12419 (2017).
19. Fazio, L. K., Bailey, D. H., Thompson, C. A., Siegler, R. S. Relations of different types of numerical magnitude representations to each other and to mathematics achievement. Journal of Experimental Child Psychology, 123, 53-72, 10.1016/j.jecp.2014.01.013. (2014).
20. Matthews, P. G., Ellis, A. B. Natural Alternatives to Natural Number: The Case of Ratio. Journal of numerical cognition, 4, 19–58. doi.org/10.5964/jnc.v4i1.97 (2018).
21. Gouet, C., Carvajal, S., Halberda, J., Peña, M. Training nonsymbolic proportional reasoning in children and its effects on their symbolic math abilities. Cognition, 197,104154. doi: 10.1016/j.cognition.2019.104154 (2020).
22. Hassinger-Das, B., Hirsh-Pasek, K, Golinkoff, R. Learning Landscapes: Playing the Way to Learning and Engagement in Public Spaces. Education Sciences, 8. doi:10.3390/educsci8020074 (2018).