Intervention approaches to remediate developmental dyscalculia informed by neuroscience

Executive summary

• In the 21^st century, lack of adequate numeracy skills can have profound negative consequences for educational success, career prospects, and overall quality of life.
• Developmental dyscalculia (DD) is a brain-based condition that leads to low numeracy skills in the context of otherwise normal intelligence and educational opportunities.
• Because of its documented brain basis, efforts towards developing effective ways to remediate DD can benefit from neuroscience findings.
• The branch of neuroscience devoted to shedding light on the development of brain processes supporting typical (and atypical) learning shows that DD can be the result of dysfunctions in multiple brain systems for math knowledge.
• Training programs designed to “stimulate” multiple aspects of math knowledge acquisition and the brain systems subserving it may, therefore, yield the best outcomes to effectively remediate math deficits in children with DD.

Introduction

In our modern, digital society, difficulties with numbers and arithmetic can have profoundly negative consequences on educational outcomes, career prospects, and overall quality of life. For instance, it has been shown that low numerical skills are a stronger predictor of poorer academic achievement than low reading skills¹. Moreover, individuals with low numerical and mathematical skills (~20% of the population) have a likelihood of unemployment that is twice that of their numerically competent peers². They are also more likely to be depressed, in poorer physical health², and have difficulties in the use of health resources (e.g., medication prescriptions, dosages)³. Finally, having poor mathematical skills has also been associated with increased rates of incarceration and decreased rates of home ownership later in life². Since low numeracy represents a massive societal problem, collective efforts in designing and developing appropriate interventions have taken on great significance, particularly over recent years.

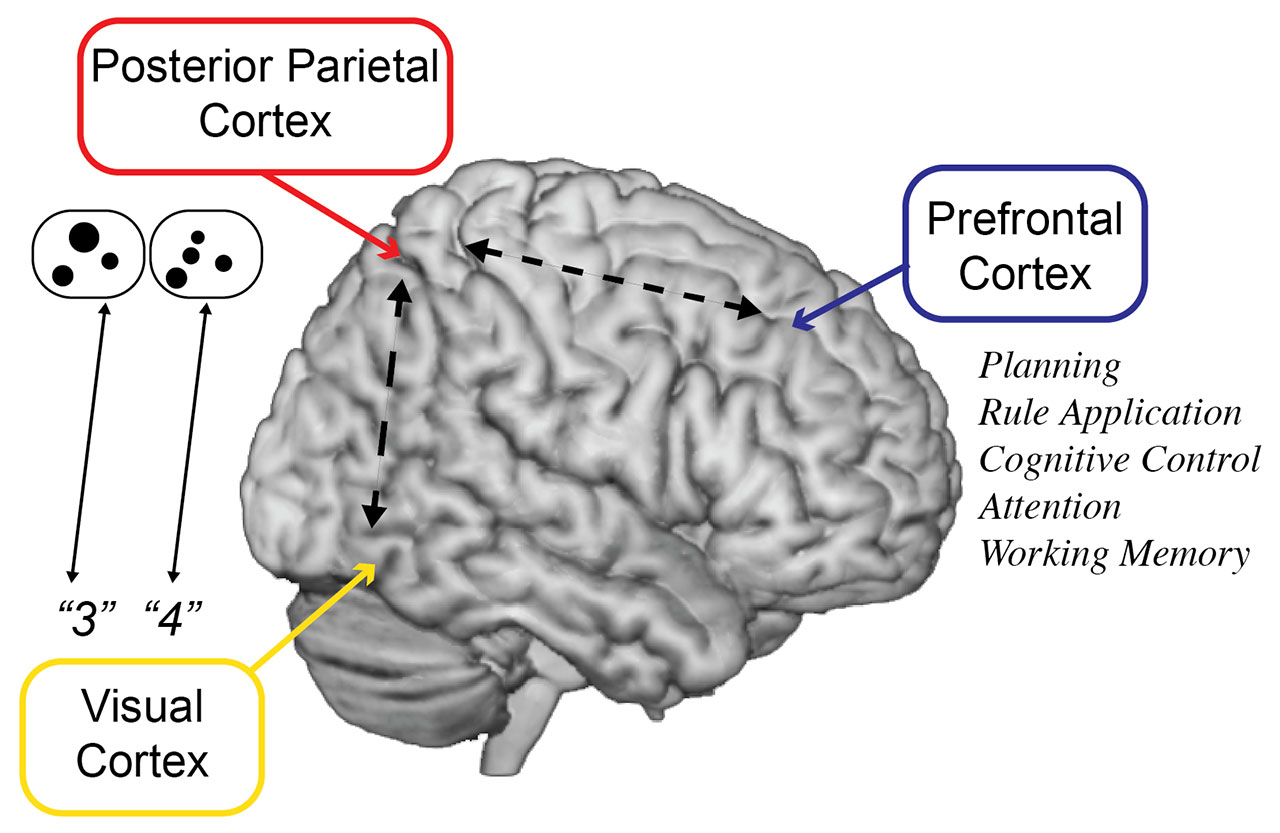
Figure 1. Multiple brain regions can be dysfunctional in DD.

A major cause of poor mathematical proficiency is developmental dyscalculia (DD), a specific learning disability that manifests in difficulties in acquiring age-appropriate numerical and arithmetical skills in the context of otherwise normal intelligence and fair educational opportunities⁴. Notably, DD has a documented brain basis⁵. Specifically, research has started to reveal that DD can be the result of deficits in one or multiple brain systems that support the acquisition of foundational mathematical competencies during the early school years (for a more in-depth review on this, see Brief “What is developmental dyscalculia and what does it look like in the brain”). Brain-based deficits in DD have been found in regions of the parietal cortex (on the lateral part of our brain) that are important for the manipulation of quantity, as well as in regions of the visual cortex (in the back of our brain) that are specialized in decoding symbols (e.g., Arabic digits) and converting them into their respective meaning (e.g., the symbol “3” to its corresponding quantity of “three things”)⁶ (see Figure 1). Moreover, in DD, deficits have also been reported in regions of the prefrontal cortex⁶, which is responsible for many goal-directed behaviours including rule learning, rule application, rule switching, cognitive control (e.g., inhibition), as well as orienting and keeping attentional focus, and juggling all these “mental actions” together (see Figure 1). Deficits in memory consolidation regions located in the inner layers of the brain (i.e., in the medial portion of the temporal lobe, within a region called the hippocampus) have also been reported in children with DD⁷. Because of its documented brain basis, part of the collective efforts focused on remediating DD has recently started to incorporate insights from the discipline of developmental cognitive neuroscience. Developmental cognitive neuroscience is a (rather new) branch of neuroscience that studies how the brain supports the typical (and atypical) development of cognitive functions—i.e., the mental processes that allow us to carry out our day-to-day activities—and, concomitantly, how the acquisition of such abilities/functions elicit changes at the brain level.

Hereafter, we report some of the findings (and corollary recommendations) that have emerged from the valuable alliance between developmental cognitive neuroscience and disciplines such as psychology and pedagogy, in their effort to provide insights for the remediation of DD. In the interest of clarity and to highlight the contribution of the brain-based aspect of a given intervention, the reported evidence is organized according to the particular brain function that was trained and tested.

Numerosity-based interventions: Training the parietal cortex

Numerosity refers to the (potentially) countable aspect of a given quantity. I say potentially because, in the case of a large set of items, its numerosity usually gets approximated rather than exactly counted—unless specifically required by the task. Numerosity manipulation is one of the processes at the core of successful math-knowledge acquisition^8–10, and there is converging evidence to suggest that this ability is hosted by the posterior parietal cortex (see Figure 1). Critically, it has been shown that, together with difficulties in dealing with numerosities and reasoning about them (e.g., being able to correctly compare the numerosities of sets)¹¹, children with DD display deficits at the level of the posterior parietal cortex. Specifically, when children with DD were asked to decide which of two sets of items was greater in numerosity while their brain activity was monitored via functional magnetic resonance imaging (fMRI) scanning, they showed less variation in the strength of their brain signal compared to a group of typically developing peers. These effects were mainly evident in the posterior parietal cortex¹².

Together, these two pieces of evidence (i.e., worse performance and weaker brain signal during simple numerosity estimation tasks) have inspired researchers to develop and test intervention programs aimed at strengthening this basic aspect of numerosity manipulation for the remediation of DD. For example, the “Number Race”—a software-based learning program—was specifically developed to foster active manipulations on numerosities in children with DD through a series of activities involving counting and numerosity comparisons¹³. After five weeks of supervised training—which occurred four days a week, for one half-hour each day—the 7- to 9-year-old DD children that were part of the study got better at those basic numerosity tasks that were the focus of the training, yet no improvements were observed in their arithmetic performance (i.e., when they were asked to solve simple addition and subtraction problems). In other words, no transfer effects to abilities that were not specifically trained were obtained¹³. This is in contrast with similar numerosity-based training programs administered to healthy adults, typically developing children, and even preschoolers. Data on typically developing groups have in fact shown that this type of numerosity-based training can produce transfer effects, actually boosting arithmetic performance^14–17. Together, this evidence suggests that numerosity-based training alone, while increasing basic numerical abilities, may not be sufficient to enhance arithmetical performance in children with DD.

Another way to support the appropriate acquisition of numerosity skills in children with DD is to focus on the ordinal aspect of numerosity, not just its cardinal one. In this sense, a training involving the mental number line has shown greater promise. After five weeks of training (five days a week for 15 minutes a day), a group of 8- to 10-year-old children with DD showed improvements both on the number-line task they were trained on, as well as on an arithmetic task (i.e., featuring addition and subtraction problems). Yet, it is worth noting that, even if children with DD showed improvements after training, their performance still differed compared to that of a group of non-DD children. Critically, after training, both groups—albeit to a different extent—showed changes in brain activity when performing the number-line estimation task, with effects evident in the posterior parietal cortex¹⁸. These results suggest that, even though this type of training could not fully rescue performance in the DD group, it still elicited transfer effects. Most importantly, such number-line training was able to induce (some) relevant brain changes even in the DD group, further highlighting the potential of this approach for remediating DD.

Symbols-to-numerosity-mapping interventions: Training the visual cortex and its connections to the parietal cortex

The ability to decode numerical symbols (e.g., Arabic digits) and to map them onto their appropriate numerosity (e.g., attaching the symbol “3” to the numerosity of “three”) represents another key aspect of acquiring numerical knowledge which is pivotal for successful mathematical learning. Dealing with the symbolic aspect of numerosity is the prerogative of the posterior parietal cortex¹⁹ but also—and in the first instance—of highly specialized areas of the visual cortex, located in its anterior part (see Figure 1). Particularly, one area called the Fusiform Gyrus (FG) has been specifically related to the perceptual decoding of Arabic digits^20–22. Most importantly, it is the interaction between the FG and regions of the posterior parietal cortex that gradually supports the automatization of an accurate mapping between Arabic digits and their numerosities—one of the core deficits of DD^23,24. Together, this evidence has inspired researchers to develop and test intervention programs aimed at remediating DD through promoting the formation of an appropriate link between symbols and their numerosities. For example, “Graphogame-Math” is a computer-based intervention program that was developed to train the association between number symbols and their corresponding nonsymbolic numerosities (e.g., arrays of dots) in a group of kindergarteners with low numeracy skills. After three weeks of classroom training (for five days, 10-15 minutes each day, supervised by teachers and in the form of play sessions), even though some (yet minimal) gains were seen on numerosity manipulation abilities, there were no improvements on arithmetic performance (i.e., no transfer effects)²⁵.

All in all, the evidence presented so far (i.e., from training studies on numerosity manipulation and symbols-to-numerosity mapping) seems to suggest that to propel significant transfer effects to arithmetical performance in DD, a stand-alone numerical knowledge intervention may not be sufficient and should instead be accompanied by the training of other—more general—mental processes that support other aspects of arithmetical learning over development.

Executive functions: Training the prefrontal cortex and its connections to the parietal cortex

Executive functions are defined as a class of cognitive processes critical to performing goal-directed and purposeful behaviours. They include the ability to plan, the ability to adequately apply rules, as well as the ability to inhibit irrelevant information, a mental process often referred to as cognitive control. Executive functions are also concerned with the ability to pay attention, and with the ability to hold and update information “on the fly,” which is known as working memory (WM). All these functions are supported by regions of the prefrontal cortex in the front of the brain, as well as by interactions of the prefrontal cortex with regions of the posterior parietal cortex (see Figure 1). Notably, the strength of the connection between prefrontal and parietal regions of the brain has been revealed as particularly important for supporting WM abilities. WM is critical to arithmetical learning²⁶ and poor WM skills have been associated with DD profiles^27,28. Moreover, brain activity during a WM task has been shown to predict subsequent arithmetical performance (i.e., two years later) in a group of 6- to 16-year-olds²⁹. Based on these findings, it has been hypothesized that WM training could potentially lead to significant (and beneficial) transfer effects to arithmetic performance. This idea was tested using an adaptive WM training program called “Cogmed working memory training program”³⁰. After five weeks of training (each day for ~40 minutes a day), the 7- to 15-year-old children that were part of the program showed some gains on an arithmetic fluency task. However, improvements were minimal and much less pronounced compared to gains on a WM task, and on a task that measured the ability to follow instructions. Moreover, this program was not specifically tested on children with DD, but on those with attention deficit hyperactivity disorder (ADHD)³⁰.

As mentioned, other types of executive functions are critical to numerical and arithmetic learning^31–34. Thus, a more effective approach may be to train multiple executive functions simultaneously. A recent study has indeed combined a comprehensive, computer-based, adaptive training program targeted at stimulating multiple executive functions, including WM, planning, and cognitive control³⁵. The training occurred in the school, for 10 weeks (with at least three sessions per week, each lasting ~15 minutes) and its effects were tested on academic outcomes of math (and reading) in a group of primary school children. The benefits of the program were evident on the multiple executive functions trained and, most importantly, also on school-grades of math (and reading)³⁵. These findings corroborate the idea that training an isolated mental function (e.g., WM) may not suffice to promote the successful acquisition of mathematical competences which, as we have seen, encompass a series of complex, computationally challenging mental processes comprising multiple steps, each requiring the orchestration of multiple brain regions and their interaction (see Figure 1).

Training the whole network: A comprehensive arithmetic training

As discussed (see also Brief “What is developmental dyscalculia and what does it look like in the brain?”), DD can be the result of deficits in multiple brain systems for mathematical knowledge⁵. Thus, a remediation program that simultaneously tackles all of them (see Figure 1) may be appropriate for successfully remediating numerical and arithmetical difficulties in DD.

Several classroom training studies have shown that combining aspects of conceptual knowledge of numbers and their relations, together with activities devoted at strengthening arithmetic problem-solving—via practicing efficient procedural strategies—can help children who struggle in numeracy lessons^36,37. A well-validated math training program that capitalizes on these principles is called MathWise⁶. In MathWise, the conceptual part of the training includes physical manipulatives (e.g., number lines) during which the child explores the relationship between the different numerosities. Critically, this phase is structured on “number families” (e.g., the “family of 5”), where the child is asked to explore all the possible combinations that “make 5” through the use of manipulatives. The conceptual part of the training also focuses on reviewing math procedures and rules (e.g., the commutative property of addition) and on delineating effective computational strategies for solving arithmetic problems (e.g., “when adding: start counting from the larger number”). During the procedural aspect of the training, the child is invited to solve arithmetical problems of progressive difficulty. Here, a series of physical math games are used [e.g., Math Bingo, where the child is asked to calculate the sum of a given problem (i.e., 6 + 5) and verify whether the answer (i.e., 11) appears on their Bingo card]. Children are also presented with activities that involve flash cards, where they are asked to solve a subset of “number family” problems covered during past lessons. A timed version of this activity is called Meet or Beat Your Score, during which the child has 90 seconds to answer a stack of flash cards comprising all sets of the “number family” problems covered during that lesson. At the end of the program, the child covers all addition problems that sum to 18, and their corresponding subtraction problems.

A recent study looked at the remediating effects of MathWise in a group of 7- to 9-year-old children with DD. The peculiarity of this study is that training effects were assessed both performance-wise, as well as brain-wise. The intervention lasted eight weeks, three times a week for 45-50 minutes each day, and it was one-on-one. The results showed that this comprehensive math training program ameliorated arithmetic performance in children with DD, and this was accompanied by overall changes in brain activity. The effects were evident in a distributed network of brain regions in the prefrontal, parietal, and visual cortices. Notably, changes in brain activity after training in DD were characterized by significant reduction of activation—to the levels registered in a group of non-DD peers—and across the whole brain network⁶. This suggests that this type of training can induce global changes across distributed brain systems that encompass multiple stages of the information processing hierarchy necessary for successful arithmetic problem solving³¹. Specifically, by facilitating the development of nonsymbolic and symbolic numerical manipulations, this type of training might place fewer demands on quantitative and visual form processes supported by the posterior parietal cortex, the visual cortex, and their interaction. Concurrently, this training might facilitate efficient mental computations by “freeing up” the cognitive load taken up by WM, planning, and cognitive control functions, supported by the prefrontal cortex. More generally, and echoing the argument above, these findings suggest that a comprehensive training which integrates conceptual as well as procedural aspects of math learning—rather than focusing on isolated components—might be more effective in remediating behavioural and brain deficits in DD.

Concluding remarks

The studies reviewed here suggest that cognitive training designed to “stimulate” multiple aspects of math knowledge (and the brain systems supporting them) may yield the best outcomes in effectively remediating math deficits in DD. Yet, we should note that some of these training programs are hard to implement at a large scale. In this sense, the advent of educational technologies could help to better distribute remediation efforts. As discussed, software-based remediation programs should be designed and developed with the idea of targeting multiple systems of knowledge. Last and foremost, they should have an adaptive component that accompanies the child at their personal learning pace, and that takes into account each individual starting point as well as specific deficit(s). To achieve this, a detailed assessment of DD should be encouraged—both at the behavioural as well as at the brain level. Finally, even though the results of the studies outlined here seem to be producing promising results, it is worth noting that remediation studies in DD are still in their infancy and, moving forward, the effort should be cohesively focused on fostering the interaction between different disciplines—including developmental cognitive neuroscience, psychology, pedagogy, and learning technologies—to design and develop well-informed, theoretically driven studies of the highest scientific standard and experimental rigour. In this sense, the implementation of randomized control trials (RCT) is necessary. A ground for this may come from participatory large-scale studies (e.g., co-created projects) where researchers and nonresearchers (i.e., teachers) team up to design, implement, and test training (or remediation) programs in well-defined groups of learners. In the long run, such studies could allow for large, high-quality data sets to be collected which can, in turn, experimentally inform ad hoc intervention programs targeted to a child’s specific needs.

References

1. Duncan, G. J. et al. School readiness and later achievement. Dev. Psychol. 43(6), 1428-1446 (2007). doi:10.1037/0012-1649.43.6.1428
2. Parsons, S. & Bynner, J. Does numeracy matter more? National Research and Development Centre for Adult Literacy and Numeracy (2005). www.nrdc.org.uk
3. Nelson & Reyna. Numeracy: a critical (and often overlooked) competence for health decision making. Ann. Behav. Med. 33, S8-S8 (2007).
4. American Psychological Association. Diagnostic and Statistical Manual of Mental Disorders: Fifth Edition. Arlington, VA: American Psychiatric Publishing (2013). doi:10.1176/appi.books.9780890425596.744053
5. Iuculano, T. Neurocognitive accounts of developmental dyscalculia and its remediation. Progress in Brain Research, 227, 305-333 (2016). doi: 10.1016/bs.pbr.2016.04.024
6. Iuculano, T. et al. Cognitive tutoring induces widespread neuroplasticity and remediates brain function in children with mathematical learning disabilities. Nat. Commun. 6:8453 (2015). doi: 10.1038/ncomms9453
7. De Smedt, B., Holloway, I. D. & Ansari, D. Effects of problem size and arithmetic operation on brain activation during calculation in children with varying levels of arithmetical fluency. Neuroimage, 57(3), 771-781 (2011). doi: 10.1016/j.neuroimage.2010.12.037
8. Libertus, M. E., Odic, D. & Halberda, J. Intuitive sense of number correlates with math scores on college-entrance examination. Acta Psychol. (Amst). 141(3), 373-379 (2012). doi:10.1016/j.actpsy.2012.09.009
9. De Smedt, B., Noël, M.-P., Gilmore, C. & Ansari, D. The relationship between symbolic and non-symbolic numerical magnitude processing skills and the typical and atypical development of mathematics: a review of evidence from brain and behavior. Trends Neurosci. Educ. 2(2), 48-55 (2013). doi: 10.1016/j.tine.2013.06.001
10. Butterworth, B. Foundational numerical capacities and the origins of dyscalculia. Trends Cogn. Sci. 14(12), 534–541 (2010). doi: 10.1016/j.tics.2010.09.007
11. Piazza, M. et al. Developmental trajectory of number acuity reveals a severe impairment in developmental dyscalculia. Cognition, 116(1), 33-41 (2010). doi:10.1016/j.cognition.2010.03.012
12. Price, G. R., Holloway, I., Räsänen, P., Vesterinen, M. & Ansari, D. Impaired parietal magnitude processing in developmental dyscalculia. Current Biology, 17(24), R1042- R1043 (2007). doi:10.1016/j.cub.2007.10.013
13. Wilson, A. J., Revkin, S. K., Cohen, D., Cohen, L. & Dehaene, S. An open trial assessment of ‘the number race’, an adaptive computer game for remediation of dyscalculia. Behav. Brain Funct. 2:20 (2006). doi:10.1186/1744-9081-2-20
14. Park, J. & Brannon, E. M. Improving arithmetic performance with number sense training: An investigation of underlying mechanism. Cognition, 133(1),188-200 (2014). doi:10.1016/j.cognition.2014.06.011
15. Park, J. & Brannon, E. M. Training the approximate number system improves math proficiency. Psychol. Sci. 24(10), 2013-2019 (2013). doi:10.1177/0956797613482944
16. Hyde, D. C., Khanum, S. & Spelke, E. S. Brief non-symbolic, approximate number practice enhances subsequent exact symbolic arithmetic in children. Cognition, 131(1), 92-107 (2014). doi:10.1016/j.cognition.2013.12.007
17. Park, J., Bermudez, V., Roberts, R. C. & Brannon, E. M. Non-symbolic approximate arithmetic training improves math performance in preschoolers. J. Exp. Child Psychol. 152, 278-293 (2016). doi:10.1016/j.jecp.2016.07.011
18. Kucian, K. et al. Mental number line training in children with developmental dyscalculia. Neuroimage, 57(3), 782-795 (2011). doi:10.1016/j.neuroimage.2011.01.070
19. Vogel, S. E. et al. The left intraparietal sulcus adapts to symbolic number in both the visual and auditory modalities: Evidence from fMRI. Neuroimage, 153, 16-27 (2017). doi:10.1016/j.neuroimage.2017.03.048
20. Ansari, D. Effects of development and enculturation on number representation in the brain. Nature Reviews Neuroscience, 9(4), 278-291 (2008). doi:10.1038/nrn2334
21. Cantlon, J. F. et al. The neural development of an abstract concept of number. J. Cogn. Neurosci. 21(11), 2217-2229 (2009). doi:10.1162/jocn.2008.21159
22. Shum, J. et al. A brain area for visual numerals. J. Neurosci. 33(16), 6709-6715 (2013). doi:10.1523/JNEUROSCI.4558-12.2013
23. Rousselle, L. & Noël, M. P. Basic numerical skills in children with mathematics learning disabilities: a comparison of symbolic vs non-symbolic number magnitude processing. Cognition, 102(3), 361-395 (2007). doi:10.1016/j.cognition.2006.01.005
24. Iuculano, T., Tang, J., Hall, C. W. B. & Butterworth, B. Core information processing deficits in developmental dyscalculia and low numeracy. Dev. Sci. 11(5), 669-680 (2008). doi: 10.1111/j.1467-7687.2008.00716.x
25. Räsänen, P., Salminen, J., Wilson, A. J., Aunio, P. & Dehaene, S. Computer-assisted intervention for children with low numeracy skills. Cogn. Dev. 24(4), 450-472 (2009). doi:10.1016/j.cogdev.2009.09.003
26. Menon, V. Memory and cognitive control circuits in mathematical cognition and learning. Progress in Brain Research, 227, 159-186 (2016). doi:10.1016/bs.pbr.2016.04.026
27. Geary, D. C. & Hoard, M. K. Learning disabilities in arithmetic and mathematics: theoretical and empirical perspectives. In: Handb. Math. Cogn., pp. 253-267 (2005). Psychology Press.
28. Iuculano, T., Moro, R. & Butterworth, B. Updating working memory and arithmetical attainment in school. Learn. Individ. Differ. 21(6), 655-661 (2011). doi:10.1016/j.lindif.2010.12.002
29. Dumontheil, I. & Klingberg, T. Brain activity during a visuospatial working memory task predicts arithmetical performance 2 years later. Cereb. Cortex, 22(5), 1078-1085 (2012). doi:10.1093/cercor/bhr175
30. Klingberg, T. et al. Computerized training of working memory in children with ADHD – a randomized, controlled trial. J. Am. Acad. Child Adolesc. Psychiatry, 44(2), 177-186 (2005). doi:10.1097/00004583-200502000-00010
31. Iuculano, T. & Menon, V. Development of mathematical reasoning. In: Steven’s Handbook of Experimental Psychology: Developmental and Social Psychology (2018) John Wiley & Sons Inc.
32. Supekar, K. & Menon, V. Developmental maturation of dynamic causal control signals in higher-order cognition: A neurocognitive network model. PLoS Comput. Biol. 8(2):e1002374 (2012). doi:10.1371/journal.pcbi.1002374
33. Soltész, F., White, S. & Szucs, D. Event-related brain potentials dissociate the developmental time-course of automatic numerical magnitude analysis and cognitive control functions during the first three years of primary school. Dev. Neuropsychol. 36(6), 682-701 (2011). doi:10.1080/87565641.2010.549982
34. Szucs, D., Soltész, F., Jármi, É. & Csépe, V. The speed of magnitude processing and executive functions in controlled and automatic number comparison in children: An electro-encephalography study. Behav. Brain Funct. 3:23 (2007). doi: 10.1186/1744-9081-3-23
35. Goldin, A. P. et al. Far transfer to language and math of a short software-based gaming intervention. Proc. Natl. Acad. Sci. U. S. A. 111(17), 6443-6448 (2014). doi:10.1073/pnas.1320217111
36. Powell, S. R., Fuchs, L. S., Fuchs, D., Cirino, P. T. & Fletcher, J. M. Effects of fact retrieval tutoring on third-grade students with math difficulties with and without reading difficulties. Learn. Disabil. Res. Pract. 24(1), 1-11 (2009). doi:10.1111/j.1540-5826.2008.01272.x
37. Fuchs, L. S. et al. Remediating computational deficits at third grade: a randomized field trial. J. Res. Educ. Eff. 1(1), 2-32 (2008). doi:10.1080/19345740701692449